| |||
|
Уважаемый старшеклассник! Вашему вниманию предлагается Заочная физико-математическая олимпиада, которая традиционно проводится Факультетом Молекулярной и Биологической Физики. Задачи, приведенные ниже, представляют собой удивительный сплав необычности повседневных жизненных ситуаций и необходимости творческого подхода к ним. Если Вы решаете такие задачи, Вы приобщаетесь к тому прекрасному и благородному, что движет физтехами уже многие годы. Если Вы можете решить такие задачи, Ваше место среди нас. Еще одной целью олимпиады является предоставление возможности попробовать свои силы в самостоятельном осмысленном использовании дополнительных источников знаний. Такие навыки необходимы настоящему исследователю, независимо от того, в какой области он применяет свой интеллект. Всем участникам олимпиады будут высланы подробные решения задач, проспекты факультета и института, дипломы участника Если Вы не смогли решить какую-либо задачу, не огорчайтесь – ведь правильное решение даже половины столь нетривиальных задач дает повод гордиться своими знаниями, а так же шанс получить почетный диплом Победителя олимпиады, что будет учитываться при поступлении на наш факультет. Решения задач следует присылать в тонкой тетради простой бандеролью по адресу:
141700, Московская обл., г. Долгопрудный, Последний срок отправки решения – 15 февраля 2002 года. На титульном листе и на отдельном листочке разборчиво укажите свою фамилию, имя, отчество, почтовый адрес, место учебы, класс. Так же просим прислать конверт формата А4 с обратным адресом и вложенными в конверт марками. В электронном виде олимпиада также доступна на сайте ФМБФ http://www.bio.mipt.ru. Заметим, что официальным вариантом олимпиады является печатная версия, и все сомнения между электронным и печатным вариантом решаются в пользу последнего. Если Вы желаете, чтобы в олимпиадах следующих лет участвовали Ваши авторские задачи, присылайте их почтой или в архивах на bio@pop3.mipt.ru Желаем успеха! © Задачи предлагали: Дёмин В., Лазаревич А., Пьянков Ю., Постоваров П., Сиденко С., Титов А., Яворский В. Часть задач взята из сборников и олимпиадного фольклора Физтеха (понравились очень). Дизайн и организация олимпиады – Яворский Владислав ФИЗИКА1. Если достаточно густой ёршик для мытья посуды наполовину вставить в пробирку и перевернуть её отверстием вниз, то при легком покачивании из стороны в сторону пробирки можно наблюдать, как ёршик все дальше входит в неё, поднимаясь, таким образом, вверх. Объясните описанное явление.
3. Из открытого сверху полусферического аквариума радиуса R, наполовину заполненного водой, с каждой единицы поверхности испаряется в единицу времени объём жидкости q. Через какое время вся вода испарится? 4. Вокруг звезды по круговым орбитам радиусов r1 и r2 вращаются две планеты (орбиты лежат в одной плоскости). Найти расстояние между планетами в момент времени, когда скорость одной планеты относительно другой направлена по прямой, их соединяющей. 5. Оболочка космической станции представляет собой зачернённую сферу, температура которой в результате работы аппаратуры внутри станции поддерживается равной T = 500 K. Количество теплоты, выделяемое единицей площади поверхности, пропорционально 4-й степени термодинамической температуры. Определите температуру оболочки Tx, если станцию окружить тонким черным сферическим экраном почти такого же радиуса, как и радиус её оболочки. 6. Шарик массой m, заряженный электрическим зарядом q, прикреплен к концу непроводящей нити. Другой её конец прикреплен к самой высокой точке кольца радиусом R, которое находится в вертикальной плоскости. На кольце, изготовленном из жесткой проволоки, равномерно распределён заряд Q того же знака, что и q. Определите длину нити l, при которой после отклонения шарик окажется на оси кольца, перпендикулярной его плоскости. 7. При изготовлении полиэтиленовой пленки широкая полоса протягивается на роликах со скоростью v = 15 м/с. Благодаря присутствию сил трения, поверхность пленки получает поверхностный заряд плотности s. Оцените максимальные значения плотности поверхностного заряда s и электромагнитной индукции B, если при напряжённости поля E = 20 кВ/см в воздухе возникает электрический разряд. 8. В цилиндрический конденсатор высоты h, внутренним радиусом R, зарядом Q, расстоянием между обкладками d < < R со скоростью v [м/с] заливают диэлектрик диэлектрической проницаемостью e. Как будет зависеть энергия такого конденсатора от времени? 9. Прозрачный цилиндрический сосуд высоты l (l < < Rc, Rc – радиус сосуда) заполнен идеальным газом с молярной массой m, температурой T под давлением p0. Зависимость показателя преломления n газа от его плотности r удовлетворяет соотношению n=1+ar. Сосуд привели во вращение с угловой скоростью w вокруг оси. Вдоль оси вращения на сосуд падает узкий параллельный световой пучок радиуса rп. Определите радиус R пятна на экране, расположенном перпендикулярно оси сосуда за ним на расстоянии L. Считать, что изменение давления газа в каждой точке сосуда вследствие вращения мало по сравнению с p0. Влиянием торцов сосуда на ход световых лучей пренебречь. 10. Точно над карандашом, расположенным вертикально над водой, находится точечный источник света. На дне сосуда с водой видна тень карандаша. Если карандаш опускают в воду, то, когда он входит в нее, размер темного пятна увеличивается. Если затем карандаш вытаскивают из воды, то на месте темного появляется светлое пятно. Объясните описанные явления. МАТЕМАТИКА1. Для того, чтобы уравнение 1/x-1/y=1/n имело единственное решение в натуральных числах (x; y) для заданного натурального n, необходимо и достаточно, чтобы n было простым числом. Докажите это. 2. Остап Бендер организовал в Нью-Васюках раздачу слонов населению. На раздачу явились 28 членов профсоюза и 37 не членов профсоюза, причем Остап раздавал слонов поровну всем членам профсоюза и поровну всем не членам. Оказалось, что существует единственный способ раздать таким образом всех слонов. Какое наибольшее число слонов могло быть у О. Бендера? 3. Доказать, что сумма длин расстояний от центра окружности до сторон вписанного в нее равнобедренного треугольника больше ее радиуса. 4. На отрезке [0;1] задано такое множество M, являющееся объединением нескольких непересекающихся отрезков, что расстояние между двумя любыми точками из M, не равно 0,2. Доказать, что сумма длин отрезков, составляющих M, меньше 0,6. 5. На доске написано число 2. Каждый из двух игроков своим ходом заменяет число n на число n+d, где d - делитель числа n, меньший его. Выигрывает тот, кто напишет на доске число 2001 (писать большие числа запрещается). Кто выигрывает при правильной игре: начинающий игру или его партнер? 6. Каждая точка окружности окрашена в один из двух цветов: черный или белый. Доказать, что в эту окружность можно вписать равнобедренный треугольник с вершинами одного цвета. 7. Каждый из учеников класса занимается не более чем в двух кружках, причем для любой пары учеников существует кружок, в котором они занимаются вместе. Докажите, что найдется кружок, в котором занимается не менее 2/3 всего класса. 8. В треугольник ABC вписана окружность, а вокруг нее описан квадрат. Доказать, что внутри треугольника лежит более половины периметра квадрата. 9. Известно, что модули всех корней уравнений x2+Ax+B=0 и x2+Cx+D=0 меньше 1. Доказать, что модули корней уравнения x2+((2A+C)/3)x+((2B+D)/3)=0 также меньше 1. 10. На плоскости лежат четыре точки, при этом никакие три точки не лежат на одной прямой. Докажите, что найдется треугольник с вершинами в этих точках, у которого один из углов не больше 45 градусов. Внимание!! Обозначения переменных величин в электронной (html) и печатной (Word) версиях различаются, желательно скачивать doc-файл, также просьба кратко записывать условия задачи для устранения недоразумений. Гостевая книга Если у вас есть предложения и пожелания - есть гостевая книга. Автор этой странички уважает интеллектуальную собственность других людей и надеется на взаимное понимание. Напишите мне письмо! Мой адрес yavorsky@mail.ru ГЛАВНАЯ СТРАНИЦА |

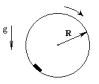 2. Полый барабан вращается с большой угловой скоростью вокруг своей оси симметрии. Внутри него помещается небольшая шайба в положение устойчивого равновесия. Найти период малых колебаний шайбы в плоскости рисунка около положения равновесия, если коэффициент трения скольжения шайбы о внутреннюю поверхность барабана равен m (m < 1).
2. Полый барабан вращается с большой угловой скоростью вокруг своей оси симметрии. Внутри него помещается небольшая шайба в положение устойчивого равновесия. Найти период малых колебаний шайбы в плоскости рисунка около положения равновесия, если коэффициент трения скольжения шайбы о внутреннюю поверхность барабана равен m (m < 1).