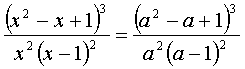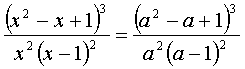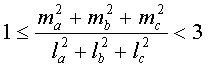Вашему вниманию предлагается Заочная физико-математическая олимпиада, которая традиционно проводится Факультетом Молекулярной и Биологической Физики. Задачи, приведенные ниже, представляют собой удивительный сплав необычности повседневных жизненных ситуаций и необходимости творческого подхода к ним. Если Вы решаете такие задачи, Вы приобщаетесь к тому прекрасному и благородному, что движет физтехами уже многие годы. Если Вы можете решить такие задачи, Ваше место среди нас.

Последний срок отправки решения - 1 февраля 2001 года. На титульном листе и на отдельном листочке разборчиво укажите свою фамилию, имя, отчество, почтовый адрес, место учебы, класс. Так же просим прислать большой конверт формата А4 с обратным адресом и вложенными марками.

1. Почему при выключении закипевшего чайника он окутывается облаком пара?
2. Представьте себе, что Земля стала вращаться вокруг Солнца в противоположном направлении, при этом направление вращения вокруг собственной оси сохранилось. Как при этом изменится количество суток в году?
3. Дана наклонная плоскость, которая составляет с горизонталью угол a . Под каким минимальным углом b _min к нормали плоскости надо бросить снизу шарик, чтобы он в некоторый момент времени покатился по плоскости? Оцените время возврата шарика в точку первого падения при b і b _min. Начальная скорость шарика v₀. Все удары абсолютно упругие.
4. Плоское тело массой m имеет форму равнобедренного прямоугольного треугольника с катетом длины L. Не прибегая к интегрированию, найти момент инерции тела относительно оси, перпендикулярной плоскости тела и проходящей через центр масс.
5. Недавно один из физтехов рассказал о своей привычке каждую пятницу выпивать один бокал шампанского. Какое максимальное и минимальное количество бокалов шампанского он мог бы выпить за февраль месяц?
6. Стакан с водой помещен в вакуум. А) Оцените скорость испарения воды с единицы поверхности воды в начальный момент времени. Температура воды T=293 К, давление насыщенных паров р_н=2,3 кПа. Б) Найти долю испарившейся воды от общей массы воды в стакане.
7. Внутри полой, непроводящей, гладкой сферы диаметра d находится маленький заряженный шарик с зарядом q и массой m. Какой величины заряд надо поместить в нижней точке сферы для того, чтобы шарик устойчиво удерживался в ее верхней точке?
8. Два мыльных пузыря радиусов r₁ и r₂ сливаются в один пузырь радиуса r₃. Найти атмосферное давление, если поверхностное натяжение мыльной пленки равно s .
9. На столе лежит металлический, электрически нейтральный куб с ребром длины 1 метр. Допустим, что мы умеем перемещать позитрон (частица с массой электрона, но имеющая противоположный заряд) внутри куба без столкновения с другими частицами. Найдите работу, которую необходимо затратить для перемещения позитрона от нижней к верхней грани.
10. Оцените, сколько горожан нужно было Архимеду выстроить на крепостной стене для того, чтобы они могли поджечь римский корабль, направив в одну точку корабля солнечные лучи с помощью плоских зеркал диаметром d=1 м, если корабль подошел на расстояние L=200 м от берега. (Для выжигания на дереве солнечными лучами надо иметь линзу с отношением диаметра D к фокусному расстоянию F больше 0,07).

1. Камера шлюза наполняется несколькими насосами одинаковой производительности. Если их все включить, они заполняют камеру за 9 часов. Рабочий шлюза включает насосы последовательно через одинаковое время и они работают до заполнения камеры. Сколько проработал насос, включенный первым, если насос, включенный последним, проработал 4 часа?
2. С помощью циркуля и линейки построить квадрат, у которого каждая сторона или ее продолжение проходит через одну из вершин выпуклого четырехугольника.
3. Найти все корни уравнения:



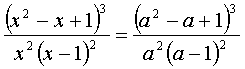
4. Дана последовательность натуральных чисел: k₀=1, k_n=1+min{2k_[n/2];3k_[n/3];5k_[n/5]}, где min – наименьшее из чисел, [ ] – целая часть числа. Докажите, что для всех nі 0 выполняется k_n>n.
5. Пусть m_a, m_b, m_c – длины медиан треугольника ABC, а l_a, l_b, l_c – длины его биссектрис. Докажите неравенство:



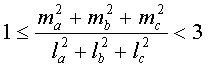
6. Последовательность многочленов задана следующим образом:

P₀(x)=1, P₁(x)=x, P_n(x)=xЧ P_n-1(x)-P_n-2(x) для nі 2.

А) Сколько вещественных корней имеет уравнение P₂₀₀₁(x)=0?

Б) Докажите, что все корни уравнения P₂₀₀₁(x)=0 лежат в интервале (-2;2)

7. Из тараканьей норки одновременно выбегают три таракана, которые начинают разбегаться по полу комнаты прямолинейно, с одинаковыми скоростями и в разных направлениях. Первого таракана студент Иванов раздавил через 1 минуту в точке А, второго – через 2 минуты в точке В, третьего – через 3 минуты в точке С. Как ему найти тараканью норку?
8. Функция f(f(f(…f(x))…))=1 при всех x (вложенность функций имеет 2001 порядок). Какое минимальное число корней имеет уравнение f(x)=1?
9. На плоскости даны треугольник, четырехугольник, …, 2001-угольник. На какое максимальное количество частей они могут разделить плоскость? Например, два треугольника делят плоскость максимум на 7 частей (“звезда Давида”).
10. Действительные числа a, b, c, d удовлетворяют условиям: 0Ј aЈ bЈ cЈ d и ad<bc. Доказать, что существует такое действительное n, что aⁿ+dⁿ=bⁿ+cⁿ.